Dripping down the rivulet: pattern formation of a thin film flowing under an inclined planar substrate

Hanging and dripping drops appear in uncountable moments of our daily experience. The foundation of our investigation lies within the theoretical framework of the Rayleigh-Taylor instability—a phenomenon characterized by the destabilization of a horizontal interface between a denser fluid and its lighter counterpart. In this scenario, the interface undergoes instability, leading to the intrusion of the heavier fluid into the lighter one. Our exploration centers on scenarios where the presence of an upper wall confines the denser fluid, forming a thin layer beneath the solid surface. The uncertain equilibrium governing this interface manifests as a balance between destabilizing hydrostatic pressure and stabilizing effects induced by surface tension.

Conventionally, a horizontal substrate yields regular patterns, often in the form of hexagons or squares. However, our study introduce a deliberate tilt which imparts a gravitational force characterized by both wall-normal and tangential components, thereby disrupting the expected symmetry through drainage. This inclination emerges as a crucial factor in averting the phenomenon of dripping — an occurrence defined by significant deformation of the interface leading to the separation of fluid phases. The nuanced adjustment of the substrate angle proves instrumental in maintaining stability and mitigating potential adverse effects within the fluid dynamics under scrutiny.

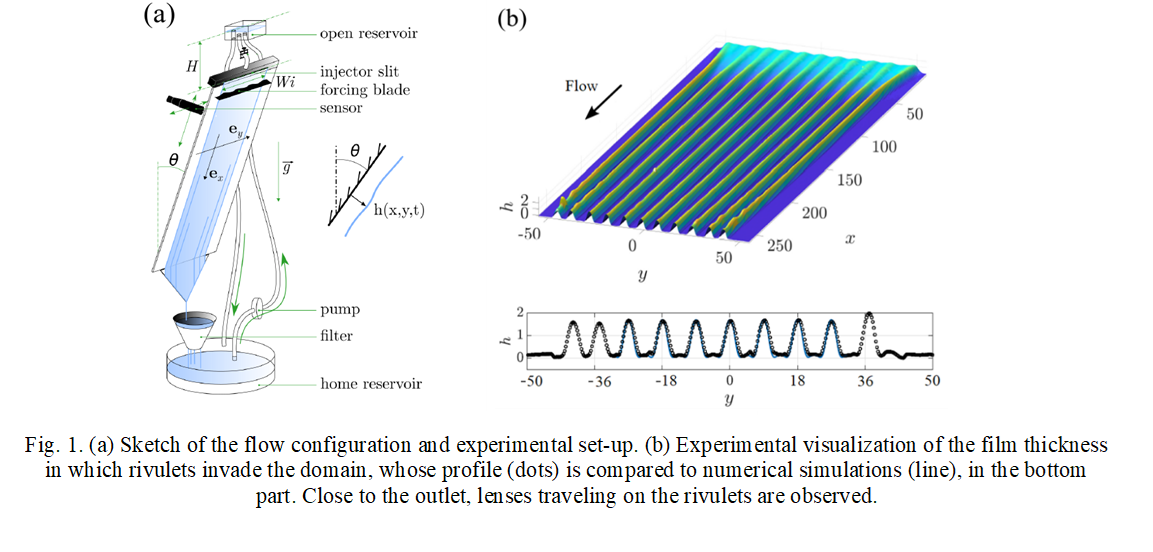
In our experimental setup, we continously infuse fresh fluid into the thin film. This dynamic replenishment facilitates a detailed observation of the spatial evolution of patterns, ultimately leading to the attainment of stationary shapes. A very viscous Newtonian fluid is injected under an inclined glass plate, with a constant flow rate. We study the dynamics of the flat film to spanwise perturbations at the inlet. Spanwise-periodic and streamwise-aligned structures, called rivulets, invade the domain, with a well-defined wavelength set by the linear dispersion relation of the flat film.

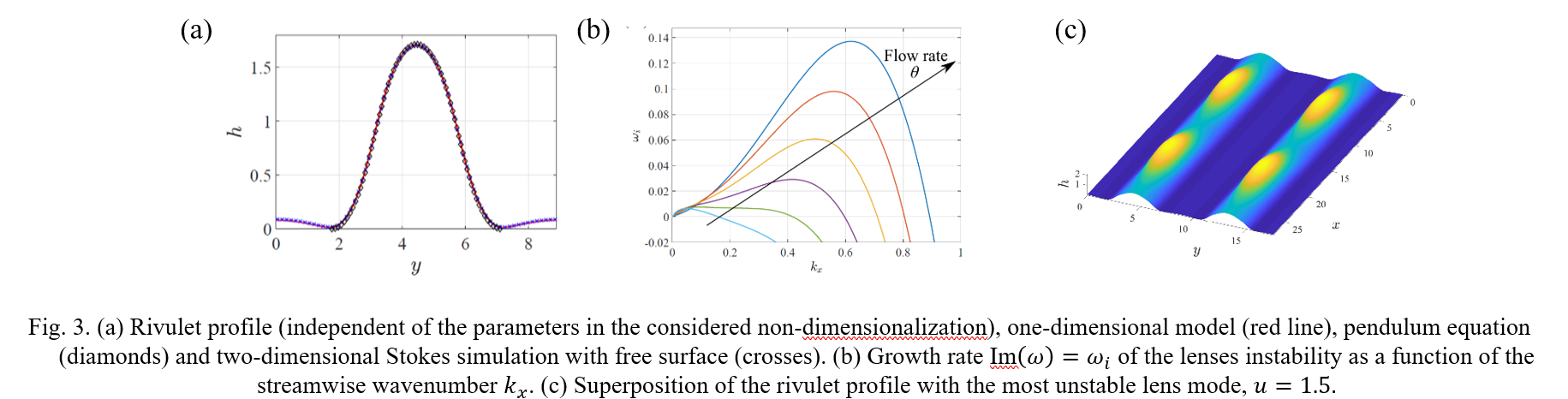
The fully non-linear evolution leads to a steady pattern characterized by rivulets. We develop a one-dimensional model that ensures the conservation of the flow rate in the cross-section. We deduce that the central lobe, of high thickness, is steady. We recover the central lobe shape via the pendulum equation, i.e. the rivulet profile is a pure equilibrium between surface tension and gravity. A secondary stability analysis on this rivulet profile with respect to streamwise perturbations reveals that the rivulets are progressively stabilized as the flow rate or the inclination angle decrease, and only very large wavelengths remain weakly unstable. As a result of the instability, lenses traveling on the rivulets are observed.

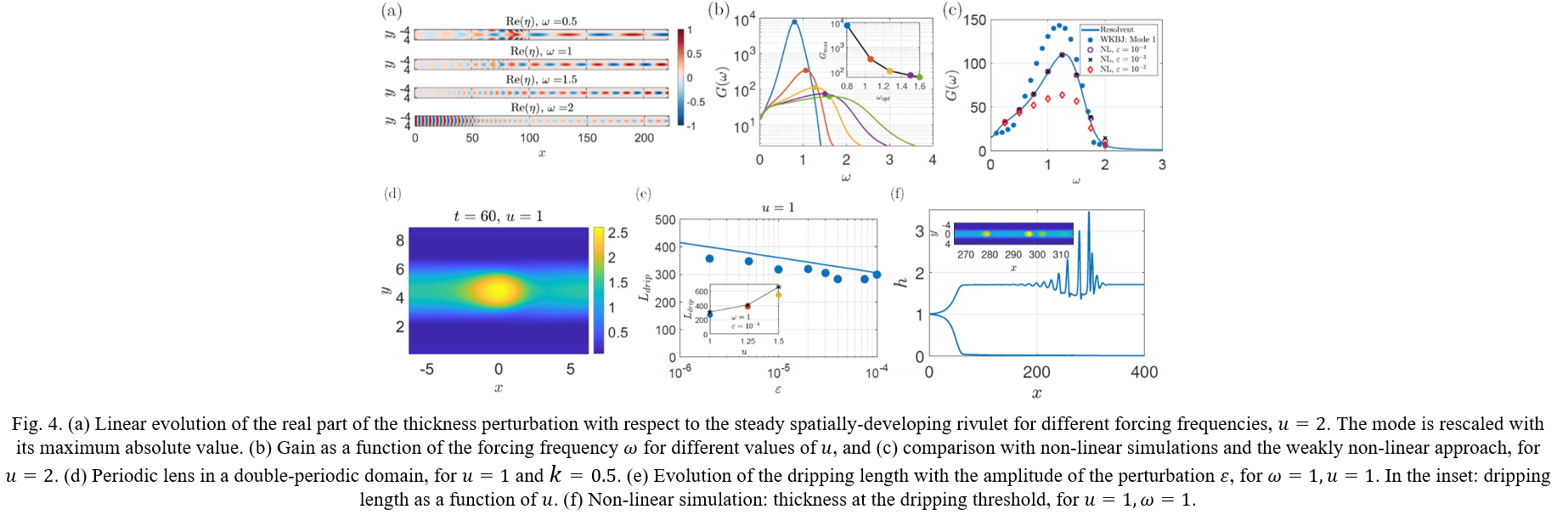
We therefore numerically study the evolution of these lens perturbations on the spatially developing rivulets, with inlet and outlet conditions analogous to the experimental setup of Fig. 1. The inlet is also temporally forced the inlet with a harmonic forcing of frequency ω. The linear response to this harmonic forcing shows that wavy perturbation evolves in lenses and perturbations are damped on the sides. We identify an optimal frequency that maximizes the amplitude of the response, which is in good agreement with a weakly non-parallel stability analysis (WKBJ) and with the non-linear simulations. We then focus on the late-stage of the growth of lenses on a fully-saturated rivulet and obtain an estimate of the dripping threshold as a function of k for this configuration. We finally combine the linear prediction and the non-linear one for fully-saturated rivulet and obtain an estimate of the dripping length in a large range of parameters, with a good agreement with the non-linear simulations.

In this analysis, we identified a possible route to dripping and a wide range of parameters for which rivulets are streamwise-saturated and steady. In the whole scenario of dripping of an overhanging liquid, these results suggest that a thin film would not immediately go from a flat state to a dripping state, but rather go by an intermediate state, i.e. rivulets that are exactly two-dimensional pendent drops. The dripping is linked to the secondary instability of the rivulet itself, more than to the stability of the flat film. We identified the ordered pattern of lenses, their amplification and we gave an estimate of the dripping length. However, when the substrate is slightly inclined with respect to the horizontal, the picture drastically changes. Pendant drops below a wet substrate accumulate fluid from the surrounding thin liquid film, often resulting in dripping. The growth of such drops is counteracted by their ability to move over an otherwise uniform horizontal film. When the substrate is slightly tilted (~ 2 deg), drops become too fast to grow and shrink over the course of their motion. Combining experiments and numerical simulations, we rationalize the transition between the conventional growth regime and the previously unknown decay regime. Using an analytical treatment of the Landau-Levich meniscus that connects the drop to the film, we quantitatively predict the drop dynamics in the two flow regimes and the value of the critical inclination angle for the transition between these regimes.

BIBLIOGRAPHY